Absolute Value Definition
In mathematics, the absolute value, also known as the modulus of real number, is defined as the non-negative number without any sign (-) used. It is written in the form of | x |. This absolute value is applied to form the zero origins to a digit of the coordinate system. We can use the absolute value on both scalars and vector quantities. A set of upward lines is used to represent absolute value, as shown in brackets (| |). For instance, the absolute value for 3 and -3 is the same |3|. For a more precise understanding, see the below diagram:
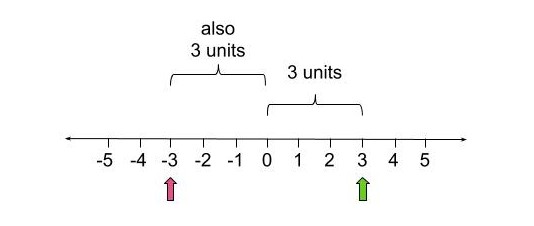
Table of Contents
Formula of Absolute Value
For a more precise understanding, let's assume x is a real number. Then the absolute value of x is determined as:
\[\left| x \right| = \left\{ {\begin{array}{*{20}{c}} {x|if|x \ge 0}\\ { - x|if|x < 0} \end{array}} \right.\]
That is,
|x| = x for a positive x
|x| = −x for a negative x (in 2nd case −x is positive), and |0| = 0.
Note:
To calculate the absolute value, you can use our Absolute Value Calculator.
Example
For a better understanding, let's have an example below:
Suppose we have an equation having absolute value, for these, let's find the value of x (real number)
Given data
Equation : |5 - 2x| - 11 = 0
To Find
Absolute Value = ?
Solution
Let's solve this equation
|5 - 2x| = -11
Now expanding the absolute value as per the above-given formula:
5 - 2x = 11 , 5 - 2x = -11
-2x = 6 , -2x = -16
x = -3 , x = 8
Let's have a simple here, Find the absolute value for -|2| and |-2|.
As we know:
|x| = −x for a negative x (in which case −x is positive)
And,
|0| = 0.
So,
-|2| = -2 and |-2| = 2
