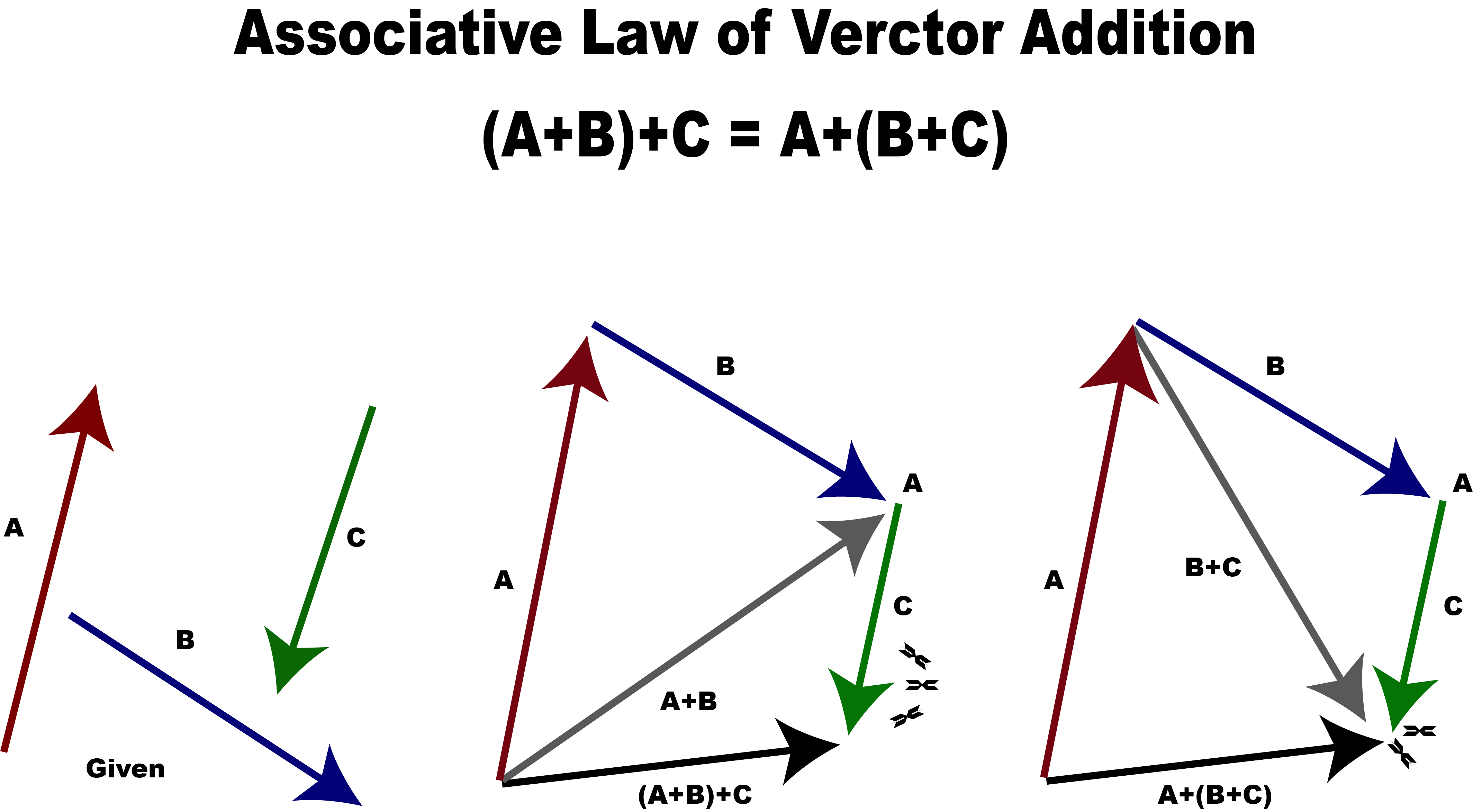
Associative Law Definition
In mathematics, an associative law is defined as the law where a group of numbers associated in brackets is solved first. However, it doesn't matter what numbers we group because the resultant answer will be the same in every state.
Note:
To calculate Gauss's law, you can use our Gauss's Law Calculator.
For Instance, adding a number (10 + 5) + 5 is equivalent to adding 10 + (5 + 5) because in both term the answer we will get is 20.
An associative law implies the same for multiplication as like addition. For instance, multiplying (5 × 4) × 2 is equivalent to 5 × (4 × 2) as 20 × 2 = 5 ×8 = 40 In symbolical form, both law addition and multiplication associative law can be written as:
-
a + (b + c) = (a + b) + c
-
a . (b . c) = (a . b) . c
However, note that you cannot use this law for subtraction because the answer for grouping the same number can be different. For Instance, subtracting a number (10 - 5) - 5 = 5 - 5 = 0 Whereas 10 - (5 - 5) = 10 - 0 = 10, 10 is not equivalent to 0.
